Exponencial

Exercícios de Exponenciais

1. Resolva a equação igualando expoentes de potências com base comum:

Solução

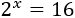
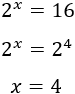
Equacionamos os expoentes das potências para o resultado de $2^x$ dando como resultado 2${}^4$ se e somente se, $x=4$. 

2.  Resolva a equação escrevendo poderes cujas bases são iguais e números primos:

Solução

3. Resolva a seguinte equação:

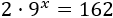
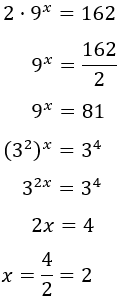
Solução:

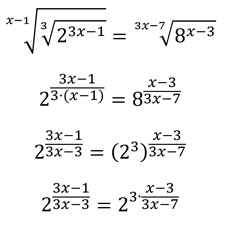
Igualando as bases:

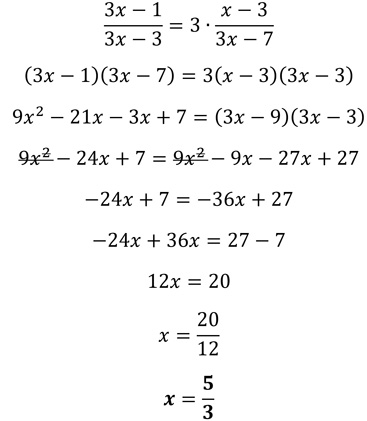
4. Resolva as seguintes equações:

a)

b)

c)

d)

Solução a:

2º método: Por inspeção simples

Para que a potência da base 2 seja igual a 16, o expoente deve ser igual a 4 e isso acontece se tomar o valor 1, portanto a solução é .

Solução para a parte b:

• Você iguala os expoentes e resolve a equação linear obtida .

  (combine os expoentes)

  (agrupe os termos semelhantes)

  (reduza os termos semelhantes)

  (isole e calcule o valor da variável)

  

Solução c:

Iguale os expoentes e resolve a equação linear obtida .

 

Solução d:

Iguale os expoentes e resolve a equação quadrática obtida .