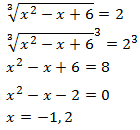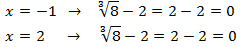Lista de exercícios:Irracionais
Uma equação irracional aparece nas raízes que contêm ou desconhecido, ou seja, ou o que está desconhecido nos signos das raízes.
Para resolver uma equação irracional, eleva-se ambos os lados da equação à ordem da raiz.
1. Resolva a equação:
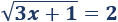
Como o radicando não pode ser negativo, \ (3x + 1 \ geq 0 \) deve ser satisfeito. Ou seja, \ (x \ geq -1/3 \).
Quer dizer,Como a única raiz que aparece é o quadrado, elevamos ao quadrado os dois lados da equação e ela desaparece:
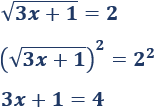
A solução da equação obtida é \ (x = 1 \). Uma vez que esta solução é maior que \ (- 1/3 \), é a solução da equação irracional.
Uma vez que esta solução é maior que, é a solução da equação irracional.
2. Resolva a equação:
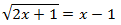
Resolução:
Como temos uma raiz quadrada, elevamos ao quadrado ambos os lados da equação. Não temos de esquecer que aplicamos a fórmula binomial ao quadrado .
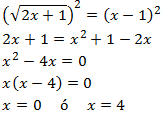
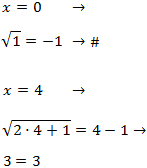
Portanto, a única solução é x = 4.
3. Resolva a equação:
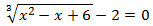
Resolução:
Como temos uma raiz cúbica, colocamos os dois lados da equação em um cubo. Para evitar ter que usar a fórmula trinomial para ou cubo, assim adicionamos -2: