Logaritmos

Exercícios de Logaritmos

1. Resolva a seguinte equação logarítmica log (x-2) - log (x-3) = log 4

Para a regra do logaritmo de um quociente escreva:

	x - 2
registro	--------	= log 4
	x - 3

Combinando os argumentos

x - 2
--------	= 4
x - 3

Assumindo x diferente de 3 (superabundante porque x = 3 já foi excluído das condições iniciais):

x - 2	4 (x - 3)
--------	= ----------------
x - 3	x - 3

Remova os denominadores
x - 2 = 4 (x - 3),

Calcule
x - 2 = 4x - 12
x - 4x = 2 - 12
-3x = -10
x = 10/3

Agora é possível verificar se a solução é aceitável, para fazê-lo, substituo x pelo valor 10/3 nos logaritmos da equação inicial e verifique se os argumentos são positivos
substituindo em log (x-2):

log (10/3 - 2) = log 4/3 o argumento é maior que zero substitua em log (x-3)
log (10/3 - 3) = log 1/3 o argumento é maior que zero.

Então, é aceitável

	10
x =	----
	3

2. Resolva a equação logarítmica:

$3 \ log {5} + \ frac {1} {2} \ log {9} - 3 \ log {3} - \ log {25}$

SOLUÇÃO

$3 \ log {5} + \ frac {1} {2} \ log {9} - 3 \ log {3} - \ log {25}$
$\ log {5 ^ 3} + \ log {9 ^ {\ frac {1} {2}} - \ log {3 ^ 3} - \ log {25}$
$\ log {5 ^ 3} + \ log {\ sqrt {9}} - \ log {3 ^ 3} - \ log {5 ^ 2}$
$\ log {5 ^ 3} + \ log {3} - 3 \ log {3} - \ log {5 ^ 2}$
$\ log {5 ^ 3} -2 \ log {3} - \ log {5 ^ 2}$
$\ log {5 ^ 3} - \ log {5 ^ 2} -2 \ log {3 ^ 3}$
$\ log {\ frac {5 ^ 3} {5 ^ 2}} -2 \ log {3}$
$\ log {5} -2 \ log {3}$
$\ log {5} - \ log {3 ^ 2}$
$\ log {5} - \ log {9}$
$\ log {\ frac {5} {9}}$

3. Resolva a equação:

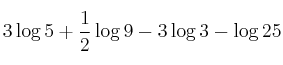
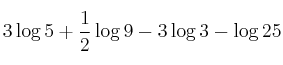
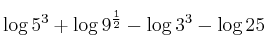
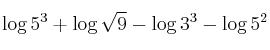
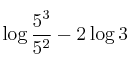
Solução:

(Aplique a definição de logaritmo )
Resolva a equação trigonométrica obtida.
(substitua as identidades correspondentes de sin2x e tanx )

(divida a equação por 2)
(Você aplica a raiz quadrada a ambos os membros)

R /

4. Resolva a equação: log x - log (x ² - 1) = - 2 log (x - 1).

Solução
Use as regras de log A - Log B = log (A / B) em log (x) = log (x ⁿ ) para reescrever a equação como.

log (x / (x ² - 1)) = log (x - 1) ^-2

Função log (x) sendo uma função um para um, podemos escrever

x / (x ² - 1) = (x - 1) ^{- 2}

Multiplique todos os termos da equação acima por (x - 1) ² e simplifique

(x - 1) ² (x / (x ² - 1)) = (x - 1) ² (x - 1) ^-2

(x - 1) ² (x / (x ²- 1)) = 1

Expanda (x - 1) ² e (x ² - 1)) e simplifique

x (x - 1) (x - 1) / ((x + 1) (x - 1)) = 1

x (x - 1) / (x + 1) = 1

Multiplique ambos os lados da equação por x + 1 e simplifique.

x (x - 1) = x + 1

x ² - 2 x - 1 = 0

Duas soluções: x ₁ = 1 + √ 2 está para 2,41 ex ₂ = 1 - √ 2 = - 0,41

x ₁ = 1 + √ 2

1) log (1 + √ 2) - log ((1 + √ 2) ² - 1) = log (1 + √ 2) - log (2 + 2 √ 2) = - log (2)

2) - 2 log (1 + √ 2 - 1) = -2 log (√ 2) = - log (2)

x ₂= 1 - √ 2

Lado esquerdo: log (1 - √ 2) - log ((1 - √ 2) ² - 1) é indefinido porque 1 - √ 2 é negativo e o termo log (1 - √ 2) é indefinido.

A equação dada tem uma solução.

x = 1 + √ 2 para 2,41